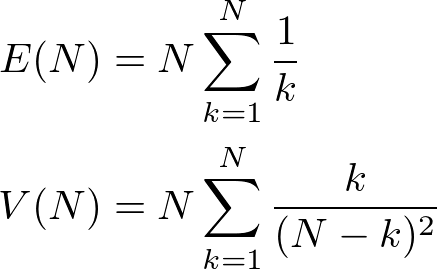
まずは、「平均で何回引けばN種類すべて入手できるのか。また、その回数のばらつきはどれくらいか。」を知りたい。ここでいう平均とは、たくさんの人が全種類入手しようと思ってこのくじ引きをするとき、a回で入手できる人、b回で入手できる人などさまざまだろうが、それらをすべて平均したら何回となるのか、という意味である。
これについては全種類の景品を集めるのに必要な回数の期待値(分析ノート:データサイエンティストのメモ書き)の記事がわかりやすい。そこにある結論を述べれば、平均E(N)と分散V(N)はそれぞれ
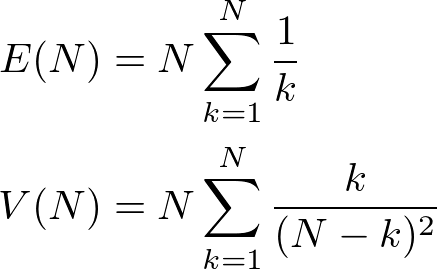
n = 4
sum = 0.0
for k in range(1,n+1):
sum += 1.0/k
print( "E = %f" % (n * sum) )
sum = 0.0
for k in range( 1,n ):
sum += k / (n - k ) ** 2
print( "V = %f" % (n * sum) )
まず、p種類入手できていて次に1回引くとき起きうる状況について、図1に示す。
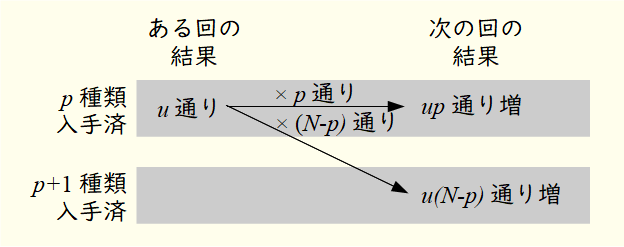
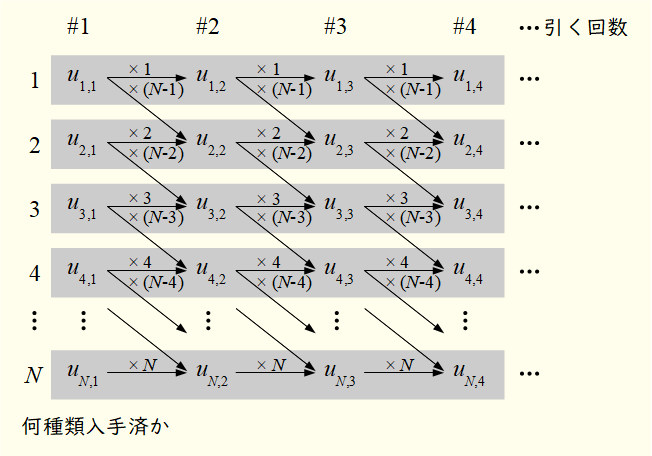
図1において、「p種類入手できているようなここまでの引きパターンの総数」はまだ具体的にはわからないから、仮にu通りあったとしている。さて、図1が示しているのは、この状況で1回引くと次のどちらかが起きる、ということである。
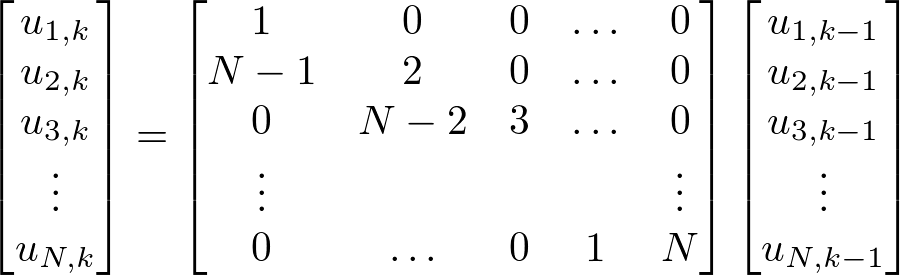
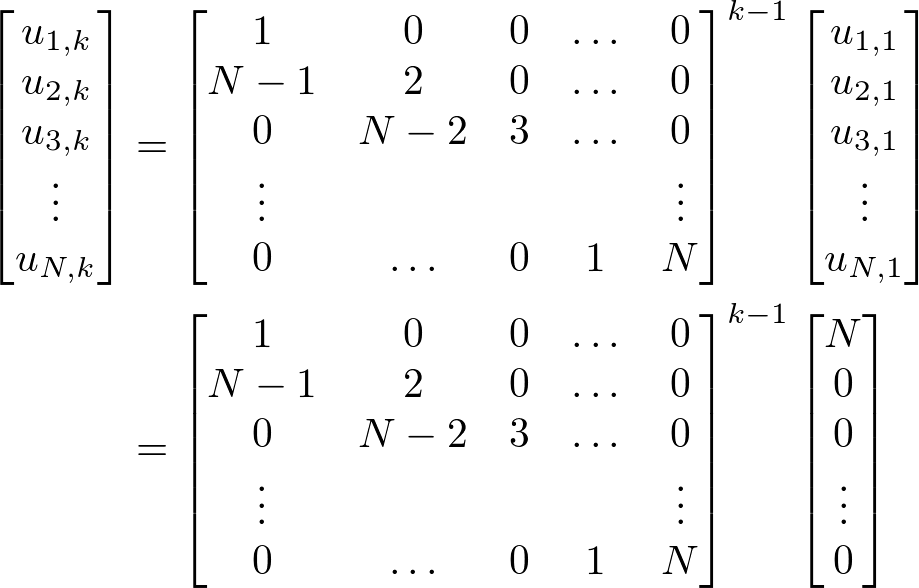
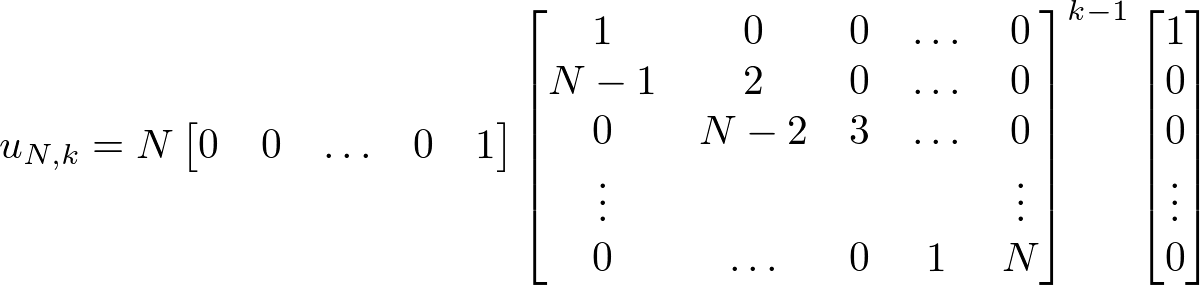
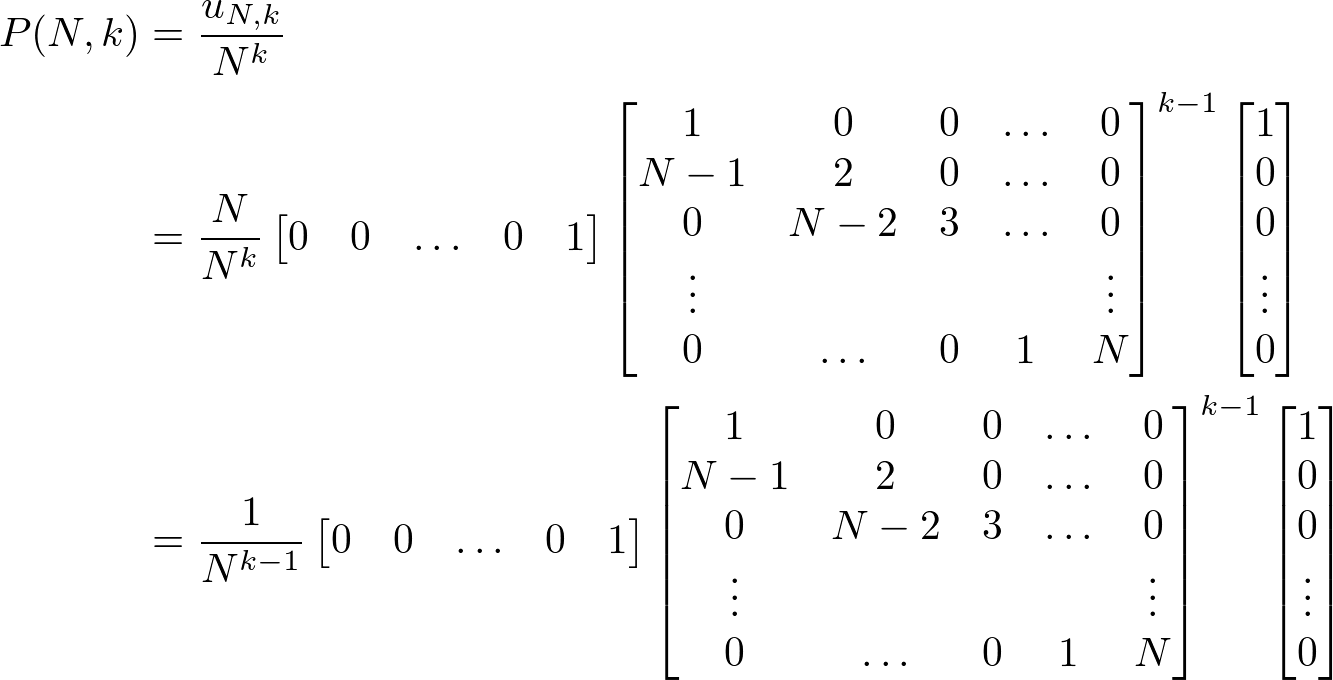
#
# n_lottery_probability.py
#
# by zhuo 2023.04.15
import numpy as np
N = 4
upto = 30
#### initialization
## initial values of u
u = np.zeros( N, dtype=float )
u[0] = 1.0
## initial values of the matrix A
A = np.zeros( (N,N), dtype=float )
for i in range( 0, N ):
A[i][i] = float(i+1)
for i in range( 0, N-1 ):
A[i+1][i] = float(N-1-i)
#### calculation
nall = 1.0
for j in range( 0, upto ):
print( "%2d\t%f" % ( j+1, u[-1]/nall ) )
u = A @ u
nall *= float(N)
上記をもとに、2種類から8種類までについて30回までの確率を計算した結果を下記のグラフ1に示す。
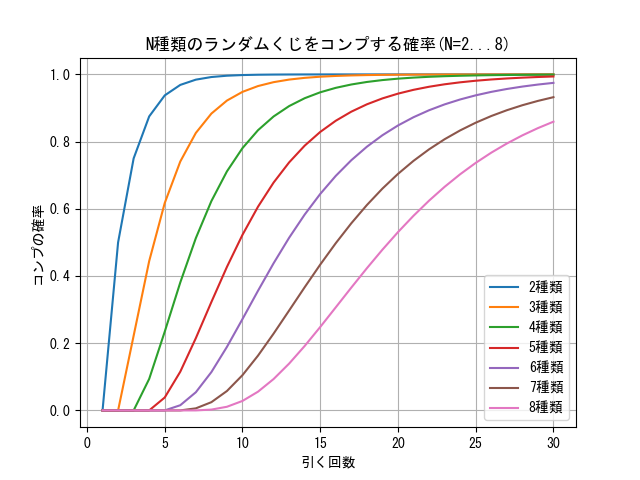
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.000000 | 0.500000 | 0.750000 | 0.875000 | 0.937500 | 0.968750 | 0.984375 | 0.992188 | 0.996094 | 0.998047 | 0.999023 | 0.999512 | 0.999756 | 0.999878 | 0.999939 |
| 3 | 0.000000 | 0.000000 | 0.222222 | 0.444444 | 0.617284 | 0.740741 | 0.825789 | 0.883402 | 0.922116 | 0.948026 | 0.965334 | 0.976884 | 0.984587 | 0.989724 | 0.993149 |
| 4 | 0.000000 | 0.000000 | 0.000000 | 0.093750 | 0.234375 | 0.380859 | 0.512695 | 0.622925 | 0.711365 | 0.780602 | 0.833988 | 0.874759 | 0.905703 | 0.929094 | 0.946729 |
| 5 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.038400 | 0.115200 | 0.215040 | 0.322560 | 0.427069 | 0.522547 | 0.606364 | 0.678003 | 0.738116 | 0.787907 | 0.828769 |
| 6 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.015432 | 0.054012 | 0.114026 | 0.189043 | 0.271812 | 0.356206 | 0.437816 | 0.513858 | 0.582845 | 0.644213 |
| 7 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.006120 | 0.024480 | 0.057702 | 0.104913 | 0.163096 | 0.228452 | 0.297307 | 0.366575 | 0.433919 |
| 8 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.002403 | 0.010815 | 0.028163 | 0.055763 | 0.093306 | 0.139321 | 0.191718 | 0.248248 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.999969 | 0.999985 | 0.999992 | 0.999996 | 0.999998 | 0.999999 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
| 3 | 0.995433 | 0.996955 | 0.997970 | 0.998647 | 0.999098 | 0.999399 | 0.999599 | 0.999733 | 0.999822 | 0.999881 | 0.999921 | 0.999947 | 0.999965 | 0.999977 | 0.999984 |
| 4 | 0.960001 | 0.969978 | 0.977472 | 0.983098 | 0.987321 | 0.990489 | 0.992866 | 0.994649 | 0.995987 | 0.996990 | 0.997742 | 0.998307 | 0.998730 | 0.999048 | 0.999286 |
| 5 | 0.862079 | 0.889101 | 0.910943 | 0.928551 | 0.942719 | 0.954102 | 0.963238 | 0.970564 | 0.976436 | 0.981139 | 0.984905 | 0.987921 | 0.990335 | 0.992267 | 0.993813 |
| 6 | 0.698004 | 0.744632 | 0.784707 | 0.818923 | 0.847988 | 0.872577 | 0.893317 | 0.910765 | 0.925415 | 0.937698 | 0.947983 | 0.956586 | 0.963778 | 0.969786 | 0.974802 |
| 7 | 0.497720 | 0.556973 | 0.611154 | 0.660094 | 0.703872 | 0.742727 | 0.776998 | 0.807071 | 0.833351 | 0.856239 | 0.876118 | 0.893344 | 0.908243 | 0.921110 | 0.932207 |
| 8 | 0.306798 | 0.365562 | 0.423102 | 0.478348 | 0.530558 | 0.579272 | 0.624250 | 0.665422 | 0.702841 | 0.736649 | 0.767044 | 0.794257 | 0.818536 | 0.840135 | 0.859301 |